In school and college examinations, final marks are obtained by summing up all the marks obtained for individual questions. However, standardized tests like GMAT, GRE have adaptive systems which make it easier to obtain average score but harder to obtain a perfect score.
A similar concept can be observed in games. Just by playing the game casually its possible to obtain 50% of the points of that level. However, it does not mean 50% effort is required to reach the first 50% of the points. The effort required is usually less than 50%. This makes it harder to obtain points as the user approaches maximum attenable points. The game developers use this trick to make the user feel gratified and play more.
This blog provides an approach to distribute score to a digital marketing account based on categories and checks before feeding it to a non-linear transformation function which makes the system adaptive in nature.
Grading System
Grading is a mechanism of judging an entity by a metric. In games applications, the grader will be based on how well the user performs in the game. For example in angry birds game, the stars are awarded based on how many of the total pigs did the user eliminate and how many of the total birds were used in the process.

In the case of games, the amount of effort required by the user to score the initial 25% of the points is less than the amount of effort required to score the final 25% of the points.
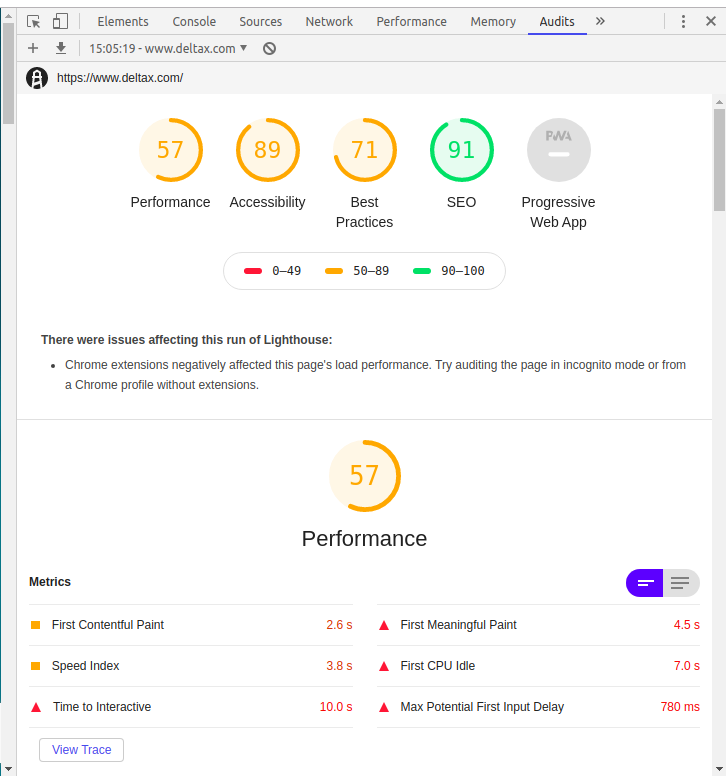
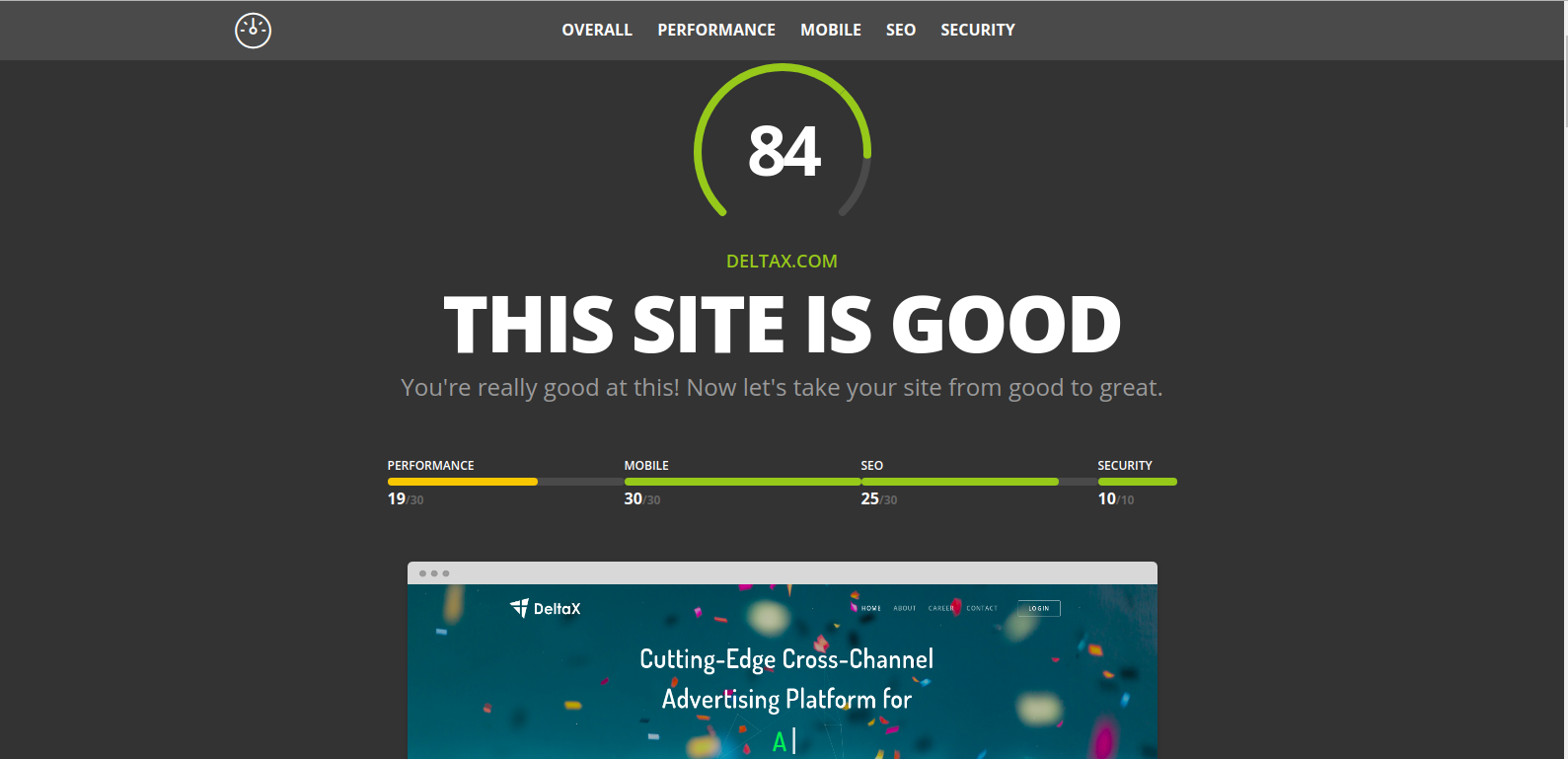
This game scoring concept can be applied to other areas. Applications which grade websites provide a score by evaluating a website based on performance, search engine optimization, and security as metrics. Finally, a score is provided by the application using the same game scoring concepts. Eg Google lighthouse, Website grader, etc.
1. Light House
2. Website Grader
Grading in Digital Marketing
Grading can also be applied to digital marketing. The objective of a digital marketing grader is to grade an account based on conventions and best practices of digital marketing.
Methodology
Conventions and best practices followed by industry digital marketers are compiled to form a series of checks for an Ad account. Each check has points associated with it, The points are distributed to checks based on the value of the check. By evaluating the check an output needs to be generated that is in between 0 and 1 inclusive.
The following set of tables provide an example of how a final score is calculated. Checks, points, evaluation output and weights are provided in the example.
| Checks | Points | Evaluation Output |
|---|---|---|
| check 1 | 30 | 0.5 |
| check 2 | 20 | 1.0 |
| check 3 | 40 | 0.25 |
| check 4 | 10 | 0.75 |
These checks are grouped into categories and weight is allocated to each category. Sum of weights of the categories should be equal to 1. Scored points of each check is calculated by multiplying the output of the check with the points associated with the check.
| Category | Checks | Points | Evaluation Output | Scored Points |
|---|---|---|---|---|
| category 1 | check 1 | 30 | 0.5 | 15.0 |
| category 1 | check 2 | 20 | 1.0 | 20.0 |
| category 2 | check 3 | 40 | 0.25 | 10.0 |
| category 2 | check 4 | 10 | 0.75 | 7.5 |
The points of the category are aggregated by summation.
The summed scored points is then divided with points for each category to obtain score ratio.
Score Ratio = Scored Points / Points
| Category | Points | Scored Points | Score Ratio |
|---|---|---|---|
| category 1 | 50 | 35.0 | 0.7 |
| category 2 | 50 | 17.5 | 0.35 |
The score ratio is then fed to a transformation function to obtain the transformed score.
Transformation function
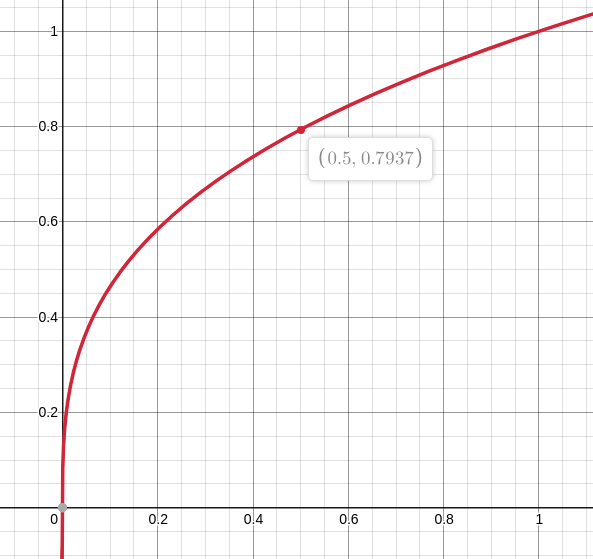
The following table is an example of a weight set for each category.
| Category | Weight |
|---|---|
| category 1 | 0.6 |
| category 2 | 0.4 |
The transformed score is multiplied by the weights of each category to obtain the penultimate score
| Category | Scored Points | Points | Score Ratio | Transformed Score | Penultimate score |
|---|---|---|---|---|---|
| category 1 | 35.0 | 50 | 0.7 | 0.887 | 0.532 |
| category 2 | 17.5 | 50 | 0.35 | 0.704 | 0.2816 |
Summation of penultimate score multiplied by 100 to obtain the final score.
Final Score = 0.813 * 100 = 81.3
The final score is the output provided by the grader to the user.
Conclusion
By introducing a nonlinear transformation function, and by feeding the function with the linear score enabled the grader to be adaptive. The result achieved: Its easier to get an average score and the difficulty keeps increasing as the score approaches 100.