Half the money I spend on Advertising is wasted; the trouble is I don’t know which half. - John Wanamaker

In digital advertising, attribution is the problem of assigning credit to one or more advertisements for driving the user to the desirable actions such as making a purchase.

Rather than giving all the credit to the last ad a user sees, attribution allows to distribute the return among contributing entities.

• Single-touch attribution gives the whole contribution to the most recent event.
• Multi-touch attribution allows more than one ads to get the credit based on their corresponding contributions.

Multi-touch attribution is one of the most important problems in digital advertising, especially when multiple media channels, such as search, display, social, mobile and video are involved. Marketers want to understand how their advertising works at the granular level.

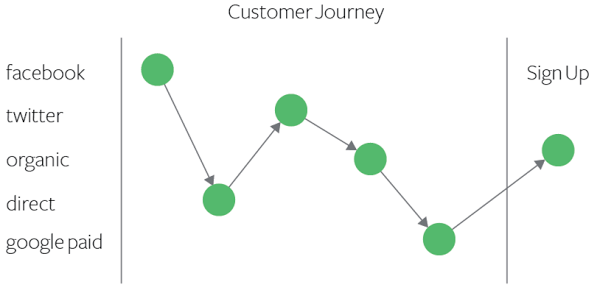
Goal is to attribute a portion of the “outcome” to all the events that contributed towards the outcome .

Marketing Events:

Impression and clicks form the sequence of events that can be termed as interaction.

Attribution Models

Rule Based

These models attribute conversion based on a well defined rule.

Image Courtesy

Last Click

Last Click is both the most commonly used model and one of the most inaccurate. The Last Click model assigns 100 per cent of revenue generated to the last customer touch point before a purchase.

First Click

In layman’s terms, First Click attribution is the polar opposite of Last Click, it attributes 100 per cent of revenue to the first consumer touch point. For example, if a customer first comes across your brand by clicking on an organic search listing, and then later spends £100 on your website, organic search is said to have driven £100 of revenue.

Last Non-Direct Click

This model is similar to Last Click, except for cases when the Last Click is a direct visit. In such cases, this model finds the latest click that isn’t a direct visit and attributes 100 per cent of the revenue to that channel instead. The rationale behind this model is the idea that once a visitor comes directly to your website they have already made the decision to buy from you, so the cause of that purchase is not the direct visit itself, but the one that pre-empted that direct visit. Linear Where the previous models deem that one part of the customer journey is solely responsible for the sale, the Linear model states that every step of the customer journey is equally responsible. It is the democratic attribution model; every touch point gets credit for an equal portion of the revenue a customer spends. Therefore, in a customer journey where the consumer had five interactions with the brand, each interaction will be credited with 20 per cent of the revenue from that customer.

Positional

While the familiar path of Awareness > Consideration > Conversion has become more sophisticated in recent years, the fact that there is a journey, which starts with a potential customer finding out about a brand, is undeniable. The Positional model acknowledges and represents this by combining aspects of First Click, Last Click and Linear. Essentially it says that the first touch point and the last touch point are worth X per cent each, and all the other touch points in between have the remaining percentage divided up evenly among them.

Time Decay

In the Time Decay model the principle is that the closer (in terms of time) a touch point is to the conversion, the more influence that touch point had on the customer decision. While the Time Decay model is one of the more sophisticated, in both implementation and understanding, this does not make it the best or the one that everyone should use.

Data Driven Attribution

In God we trust, all others bring data. - W. Edwards Deming

We want to treat attribution as a computer science rather than marketing science problem. We have data regarding user journeys which led to conversions and those which didn’t lead to. We can use this data to figure out weights that should be allocated to various channels involved.

Modelling attribution as Markov Chains

Markov process is any process that satisfies the Markov property which is given present state of the systesm its future and past states are independent.

Markov chain is a type of Markov process that has discrete state space. User journeys are typically composed of finite number of touchpoints. These touchpoints can be considered as different states of a Markov process with final state marked as conversion.

Taking inspiration from this blog we also planned to model user journeys as a chain in a directed Markov graph.

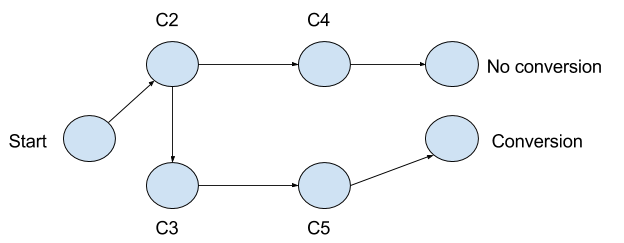
This represents an example user journey.

We decided to store pair of states e.g (s, c1) will form pair where s stands for Start state and c1 represents a particular campaign. Add c and null for success and failure respectively which in our case is getting a conversion or not.

def first_order_markov(user_indices, user_journeys):
    pairs = [] # store pairs, memory-free markov

    for i in range(len(user_indices)):
        user = user_indices[i]
        campaigns = data.loc[data.PathToConversionUserId == user, 'CampaignId'].values
        user_paths = user_journeys[i]

        campaign_index = 0

        for path in user_paths:
            for i in range(len(path) - 1):
                first = campaigns[campaign_index]
                second = campaigns[campaign_index + 1]
                campaign_index += 1

                pairs.append((first, second))

            if len(path) == 1:
                pairs.append(('start', campaigns[campaign_index]))

                if path[0] == '1':
                    pairs.append((campaigns[campaign_index], 'c'))
                else:
                    pairs.append((campaigns[campaign_index], 'null'))

                campaign_index += 1

            else:
                pairs.append(('start', campaigns[campaign_index - len(path) + 1]))

                if path[len(path) - 1] == '1':
                    pairs.append((campaigns[campaign_index], 'c'))
                else:
                    pairs.append((campaigns[campaign_index], 'null'))

                campaign_index += 1

    return pairs

This method takes in user journeys and creates pair of states. Now we will create a transition matrix which would represent the probability of reaching a start from other state based on the pairs we just formed, so for any pair of states we calculate count of occurences over all journeys in which the two nodes were part of.

count_pairs = Counter(user_journeys_with_campaigns)

def path_with_state_involved(state):
    return len([state for state_ in user_journeys_with_campaigns if state == state_[0]])

def path_with_pairs(pair):
    return count_pairs[pair]

def get_transition_matrix(unique_campaign_ids, num_touchpoints):
    states = ['start'] + list(unique_campaign_ids) + ['c', 'null']
    transition_prob = np.zeros(shape=(num_touchpoints, num_touchpoints))

    for i in range(num_touchpoints):
        count_paths   = max(1, path_with_state_involved(states[i]))
        for j in range(num_touchpoints):
            count_success = path_with_pairs((states[i], states[j]))
            transition_prob[i, j] = count_success / count_paths

    return transition_prob

def get_path_prob(graph, path):
    product = 1
    for i in range(len(path) - 1):
        product *= (graph[path[i], path[i + 1]])

    return product

def get_prob_convert(graph, paths):
    return np.sum([get_path_prob(graph, path) for path in paths])

I am skipping the code where we find all paths from start to conversion as it is trivial.

Probability of getting conversion via a path is just multiplication of transition probabilities of all the nodes involved in that path and the probability of getting a conversion is just the summation over probabilities of all paths that led to conversion.

def removal_effect(graph, campaigns, prob_convert, conversion_state):
    effect = {}

    for campaign in campaigns:
        removed_campaign = graph.copy()
        removed_campaign[:, campaign] = 0. # removing campaign/touchpoint
        paths = find_all_paths(removed_campaign, 0, conversion_state)
        prob_convert_without_campaign = get_prob_convert(removed_campaign, paths)
        effect[campaign] = (1 - prob_convert_without_campaign / prob_convert)

    return effect

Then we will remove every campaign/touchpoint from the graph and calculate the probability of getting a conversion. This will give us an impact of removing this campaign/touchpoint from the flow which we would be indicative of weights that should be assigned to this campaign/touchpoint. These weights will be used when we are trying to attribute a conversion.

Overall this was an attempt to model the attribution process using Markov Chains and getting meaningful weights out of it. Next step would be to optimize the process and make it usable.

References:

• Attribution Modelling using Markov Chains
• Attribution Theory
• Attribution Models
• Markov Process