What is feedback control ?
Feedback works by constantly comparing the actual behavior of a system to its desired behavior. If actual behavior differs from the desired one a corrective action is applied to counteract the deviation and drive the system back to its target. This process can be repeated constantly as long as the system is running.
Advantages of using the feedback control:
-
It requires relatively little knowledge about the controlled system. It only needs to know in which “direction” to nudge the system when it has gotten off its course.
-
It is not prone to external disturbances.
Case Study
Let’s take a example where we might apply the feedback control to control the process. Here is a scenario
- We are in charge of a system that allocates budget to different components ( campaigns or ad groups ) to spend on a particular day.
- This system maintains a buffer of budget as it might not be able to spend what was allocated to it.
- At each time step ( which can be after an hour or a day ) the components consume some amount of budget allocated from this buffer.
- We cannot directly assign budget to components but instead we can change the total budget allocated to these components.
- Once budget gets allocated among different components we can no longer influence the expenditure, the money will get spent owing to factors beyond our control.
- The budget that gets allocated to a particular component fluctuates randomly.
- At each time step, we need to decide if we want to allocate more total budget in order to make sure the participating components are not starving for money.

So the challenge in front of us is to control the total budget in presence of factors that we can’t even manipulate directly.
Proposed Solution
Introduce this notion of steady state which is rate of influx of money into the system is equal to the rate of expenditure of the system.We can therefore calculate measure the average amount spent by the system at any time step and we add that amount into our total budget. In the long run things should just work out. Right ?
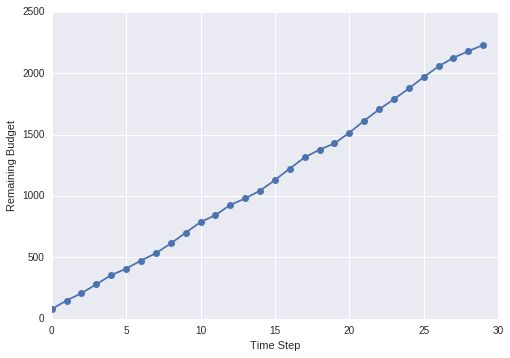
No, turns out when we do this remaining budget will keep on getting piled up. This means that we are unnecessarily putting money into the system even though the system is not capable to spend that money so finding a better solution becomes a priority.
How to control the process ?
So we cannot just rely on the average rate of expenditure but instead we should we monitor money left in the system from moment to moment. So we ask from our advertiser to give us a target as to how much money is acceptable as Remaining Budget. We can then compare the actual remaining budget with the target and adjust the total budget properly. Here we are just trying to sense the direction in which to nudge the process. But we must also take care of the magnitude of the deviation as if the actual remaining budget is only slightly below target, we will add less amount than if it is way off the mark. We will use the following formula to calculate the amount of money to be added:
Amount of money to add = k · (target – actual)
k is a numerical constant and its value can be calculated empirically.
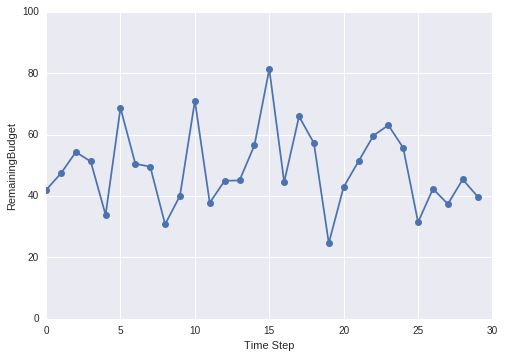
As you can see we are able to stabilize the system to some extent, just by tracking the difference in the target vs actual remaining budget. But there is one problem with this strategy, our corrective action is based on the magnitude of the deviation from the target value which means that if deviation is small the corrective action is small too. For instance, if we set k = 0.5 and choose 50 as target and current remaining budget is 40 then corrective actions is 0.5 * (50 - 40) = 5. If current expenditure is also 5 then we will never be able to bring the remaining budget to desired value. We can overcome this by increasing the controller gain k but then result might overshoot sometimes by an unacceptable amount. Solution is to magnify effect of persistent small deviations by adding them up.
Amount of money to add = k p · error + k i · cumulative error
Now we have to worry about: kp that is proportional to error and ki that is proportional to cumulative error.
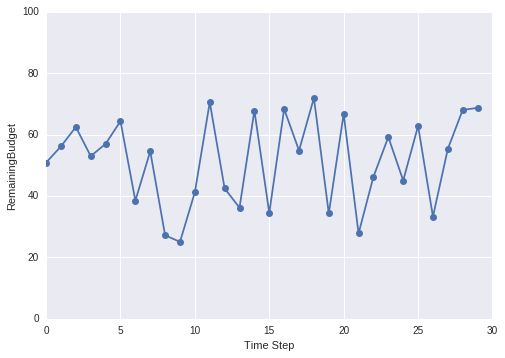
As you can see that we are able to stabilize the system just by tracking error and taking care of the cumulative error.
Summary
- Feedback control is about control and not about optimization.
- Feedback is about tracking a given reference signal, without a reference signal, there can be no feedback control.
- Some examples of applications of feedback control:
- Cache: If tracked metric is hit rate, and configurable variable is cache size ( maximum number of items that the cache can hold ), then we can use feedback control to control the hit rate.
- Queuing system: If tracked metric is the waiting time, and the adjustable parameter is the number of workings serving the queue.
I have just scratched the surface of the theory behind the feedback control but hope that this can provide to check out more about feedback control and its various applications.